Jak byście nie wiedzieli to spin dotyczący ROG już lata od wczoraj. To jeden z przykładów.
#polityka
maximilianan
★Mistrz
- 5440wpisy
- 40156komentarzy
i najgorsze jest to,ze taki belkot na ludzi dziala
Nawet nie musza sie wysilac
Zaloguj się aby komentować
Migrena ty bulwo.
#zdrowie
@maximilianan migrenę to miała Izabela Łęcka, ciebie poprostu lab napierdala 😉, mnie wczoraj też napierdalał
Współczuję... Już teraz miewam bardzo rzadko, ale kiedyś potrafiłem mieć co tydzień... Tylko że ja to mam j⁎⁎⁎ny komplet atrakcji, z przykurczami mięśni, ślepotą i zaburzeniami włącznie
@maximilianan Czy wiesz, co u Ciebie wyzwala migreny? Niektórzy mają związane z jedzeniem na przykład (podobno sery?). Mi dojście do tego, co u mnie je powoduje, zajęło około 10 lat.
Jak się okazało, jestem po prostu uczulony na pracę - a dokładniej, na narzucony na siłę rytm snu. Od czasu, kiedy wstaję od razu po przebudzeniu (żadnego spanka rano, nawet jak nie mam nic do zrobienia muszę wstawać) i idę spać kiedy mam ochotę (żadnego zostawania na siłę, jak jestem śpiący - muszę iśc spać, nawet jeżeli jest 3 po południu... albo 3 rano), właściwie nie mam już migren. Tylko czasem parę tygodni po podróżach, bo oczywiście trzeba się dopasować do środków podróży.
Zaloguj się aby komentować
Zaloguj się aby komentować
@maximilianan heheszki czy nie, ale ja to już kilka lat temu powiedziałem, że publiczna rozmowa została totalnie sparaliżowana przez takich patologicznych fact checkerów i innych deboonkerów. Teraz jeszcze na to boty na sterydach doszły ze swoimi urojeniami.
Zaloguj się aby komentować
Czaicie, że największe polskie media tak clickbaituja, że "Niemcy drżą" oznacza, że jakaś burmistrz wypizdowa ma osobisty problem?
Tak btw to w Niemczech wszyscy mają wyjebane na tamte rejony xD to tak jakby ukraińskie media mówiły, że sołtys pizdzichowa ma problem xd
#niemcy #polityka
No ale można szerzyć narracje jakoby to było stanowisko całego rządu tych złych niemiec XD
Dobrze wiedzą, że ludzie czytają tylko nagłówki w necie i z tego korzystają.
@maximilianan ja to się nie przejąłem tymi fantastycznymi wieściami o ropie. Pewnie będzie jak z gazem łupkowym
@maximilianan Dlatego warto poszukać u źródła i przekonać się czy to naprawdę clickbait. Ale komu się chce szukać.
Zaloguj się aby komentować
@Seele jest potencjał
@maximilianan kitkuuuuu!
Zaloguj się aby komentować
Powiedzmy sobie szczerze, przyszedłeś tu tylko po to, żeby pocałować Gomeza w d⁎⁎ę.
#gothic #cytaty
To może tak: twój ojciec zabawiał się z owcami
@maximilianan No i coś mi narobił? Teraz mi się jeszcze bardziej chce grać a Mroczne Tajemnice 2.5 nadal nie wyszły (╯ ͠° ͟ʖ ͡°)╯┻━┻
Zaloguj się aby komentować
Ależ ofertę znalazłem XD 1400 brutto, własne auto i spanie w kabinie XD
#pracbaza #bekaztransa
to ja mam tyle samo za bycie korposzczurkiem i opierdalaniem sie pol dnia
i to w p0lsce
@maximilianan spanie w kabinie i sranie pod kołem
@maximilianan jednego się w Niemczech nauczyłem, że nie ma większego raka niż polski pośrednik kombinujący z niemieckimi umowami. Totalna kombinacja, praca na granicach prawa, często brak praw. Już lepiej z tym translatorem bezpośrednio do Niemca pojechać i próbować sobie coś ogarnąć.
Zaloguj się aby komentować
Ale sobie właśnie sam łeb rozjebałem.
Transformacja Fouriera to tak naprawdę działanie polegające na szukaniu konkretnych częstotliwości, które odjęte od fali bazowej znacząco jej nie zmienią
#matematyka
@maximilianan Dołączę się do @pierdonauta_kosmolony i zapytam o tę falę bazową. Bo z Twojego wpisu wynika, że coś zrozumiałeś, ale niekoniecznie poprawnie.
Poza tym, odejmowanie niektórych częstotliwości (szczególnie np. wysokich harmonicznych) nie zmienia znacząco rezultatu, ale odjęcie głównych już tak.
wytrzezwiej i pomysl jeszcze raz
@maximilianan w ten sam sposob dziala FTiR? Pytam bo jestem lajkonikiem w kwestii fizyki a pracowalem sporo z FTiR. Ale tylko jako badanie próbek. Żadnego maintanance sprzętu i grzebania w metodach, wiec nie musiałem wiedzieć nic wiecej.
No i metoda analizy jest dość nudna xD
Zaloguj się aby komentować
@maximilianan myślę o liczbie 24. O jakiej liczbie myślę?
Zaloguj się aby komentować
Co to za po⁎⁎⁎⁎ny timeline, że ostoją normalności okazuje się Najman :v
#polityka
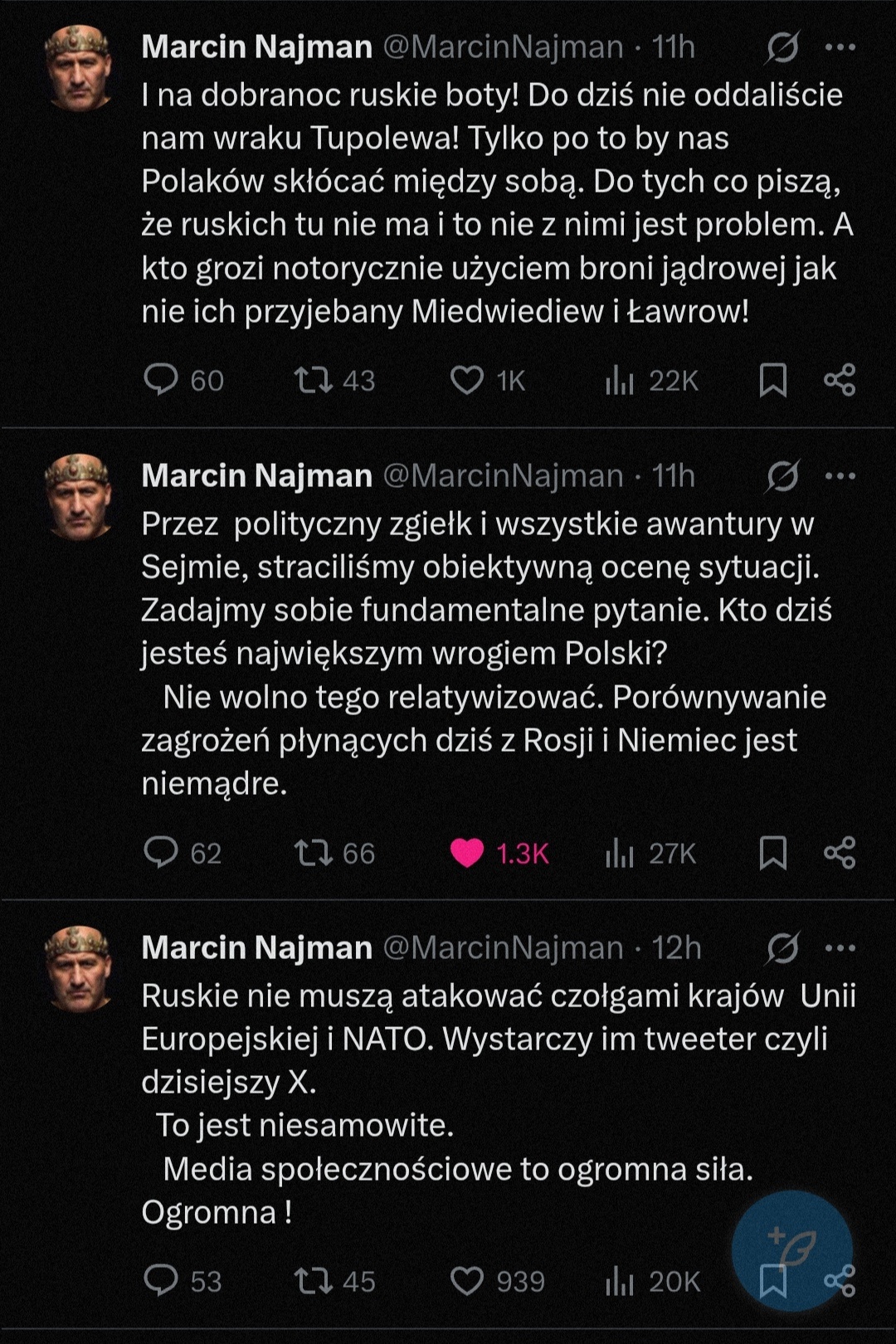
@maximilianan ksysio stanowski to pisobot, a Najman pisze z sensem. Faktycznie, coś w tym matrixie gdzieś podzieliło przez zero...
@maximilianan Z ostatnim się nie zgodzę, nie wystarczy X, potrzebni są jeszcze politycy kamerdynerzy z POPiSu którymi wszyscy w koło gardzą, łącznie z Zieleńskim. Konfa jest tu tylko naturalnym robakiem rozkładającym trupa III RP w nowym porządku świata.
Jeżeli ktoś nie wie w czym rzecz to niech sobie posłucha (tdlr: polscy politycy i biurokracja jako strażnicy starego sytemu który nas pogrąży) https://www.youtube.com/watch?v=ie7ZuVsyQH4
ostoją normalności okazuje się Najman :v
@maximilianan przecież Najman zgrywa tylko publicznie idiotę pod freaki. Inteligencja się nie sprzedaje to orze jak może.
Zaloguj się aby komentować
Osobiście uważam, że jest to najlepszy akapit w polskim rapie.
Druga zwrota chłopak bo zaczynam z d⁎⁎y strony
Masz kobietę pokaż to zostaniesz wyjaśniony
Poroniony świat od lat zboczenia są plagą
Jak tak może goły chłop z gołą babą nago
#poezja #kuki #muzyka #polskirap
@maximilianan to chyba Geli Pappon nie słyszałeś guwniarzu
Zaloguj się aby komentować
Gorąco polecam https://zglosdewelopera.pl/
Zgłosiłem dzisiaj jednego pośrednika, który uznał, że jak sam se wrzuca ofertę na FB to go nie dotyczy ustawa o jawności cen XD
Jak tylko coś takiego zobaczycie to zgłaszajcie śmiało!
#nieruchomosci #prawo
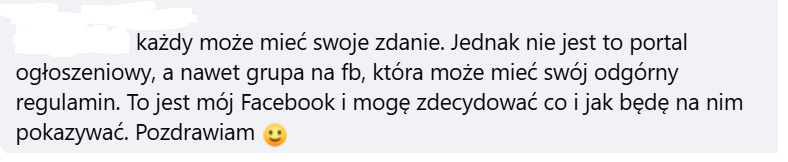
@maximilianan xD To jest jego fejsbuk xD Stawiam, że tak samo te -naście lat temu wysyłał jakieś śledzikowe łańcuszki, że nie zgadza się na to, żeby fejs wykorzystywał jego zdjęcia
Zaloguj się aby komentować
@maximilianan ... oprócz tego ludzie...
Wszystko co ktoś mówi przed słowem "Ale" jest gówno warte.
@maximilianan Pokaż co jest po ale bo tak jak napisał jeden z komentujących wszystko przed jest nie ważne.
Zaloguj się aby komentować
Mam ogromne długi, ale gdybym znalazł pracę to by mi zabrali MOJE pieniądze, a ja nie chcę, więc nie pójdę do pracy i co mi zrobicie XD
Gość wprost się przyznał do unikania spłaty zadłużenia i nic mu za to nie zrobią.
#polityka #bekazprawakow
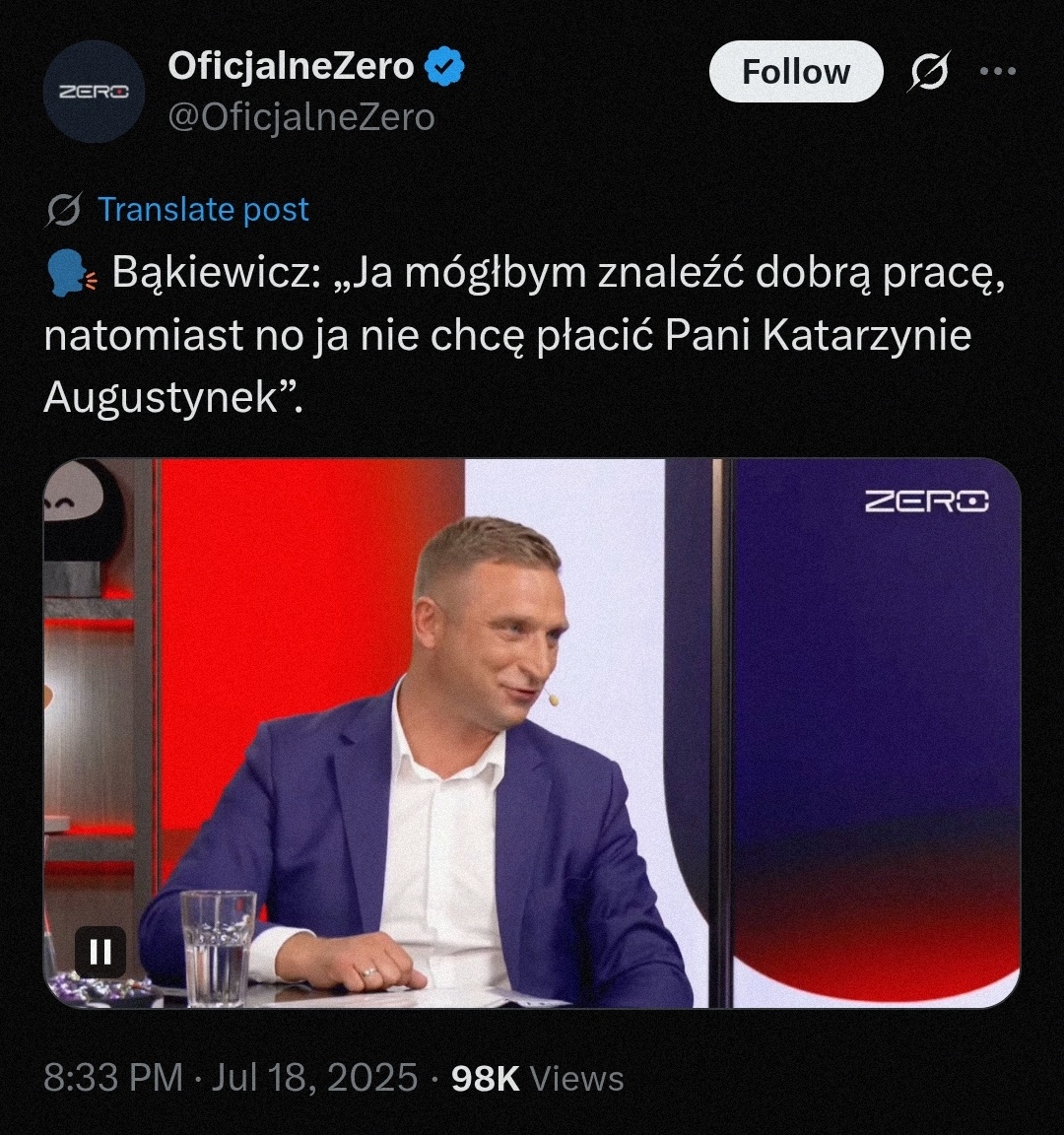
@maximilianan Setki tysięcy ludzi w Polsce robi to, co Bąkiewicz i też im nic za to nie grozi. Taki kraj, cwaniactwo jest popierane.
Jeśli faktycznie to powiedział to jest to art 286. Pożyczał z zamiarem nieoddania a to jest oszustwo. Na miejscu jego wierzycieli składałbym zawiadomienie do prokuratury może drugi prezydent by go nie ułaskawił.
Zaloguj się aby komentować
Mogły wspierać? Oni dosłownie wypuszczali ulotki z mordami pisowcow, stawiali banery z "sukcesami" rządu i finansowali pikniki pisu XDD
Oczywiście sędzia Marciniak z PKW nie widział w tym problemu.
#polityka
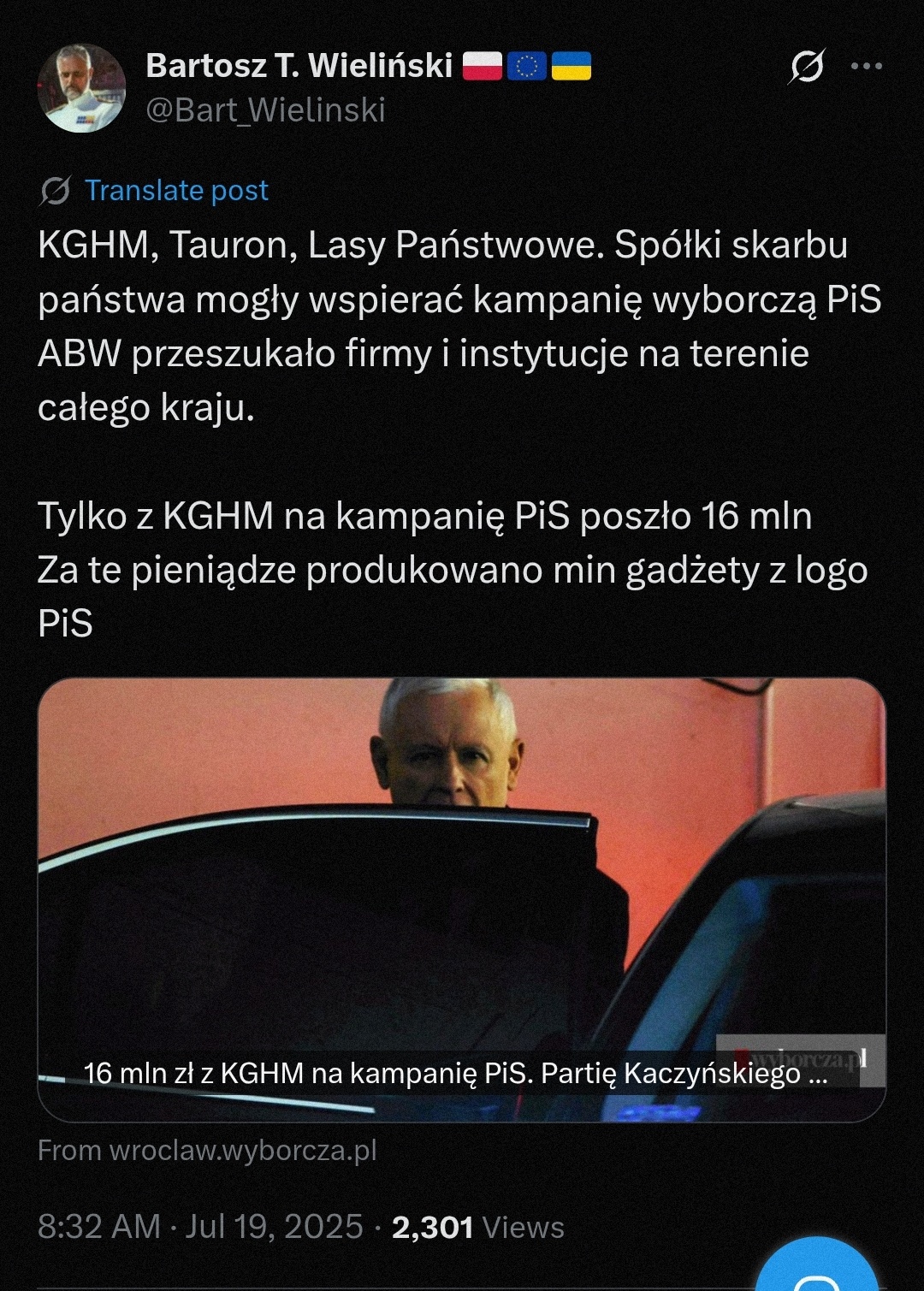
Mówiłem, że pis to mafia zanim to było modne.
Komentarz usunięty
@maximilianan a wszystko Dla Zdrowia Polaków ( ͡° ͜ʖ ͡°)
Zaloguj się aby komentować
Patrzcie jakie to proste! Jeśli przyjąć, że ksenofobia nie jest ksenofobią, tylko czymś zupełnie innym to możemy uznać, że tak rozumiana ksenofobia jest dobra! Jeśli zaś przyjmiemy, że rasizm to nie nienawiść do obcych ras czy kultur, tylko ciekawość i pewien zdrowy dystans to też wyjdzie, że jest git!
#polityka #bekazprawakow
@maximilianan
Wojna to pokój, wolność to niewola, ignorancja to siła.
@AdelbertVonBimberstein Niestety mam wrażenie, że coraz bardziej.
ludobójstwo to tak naprawdę ostrożność przed zwiększaniem populacji
@festiwal_otwartego_parasola hm, dziwne. Mógłbym przysiąc, że jeden taki malarz akwarelista miał podobny punkt widzenia na jedną sprawę...
Ja na przykład myślę, że islamofobia jest dobra i trzeba ją pielęgnować. Boję się zakazów występujących w kulturze islamu. Boję się o prawa kobiet, prawa gejów, prawo do wolności wyznania. Boję się kulturowego supremacyzmu i przyzwolenia na przemoc wobec obcych. Więc jak nie lubię jednej obcej kulturowo grupy za ich ksenofobię to też jestem ksenofobem?
@lurker_z_internetu i myślisz, że istnieje ryzyko wprowadzenia takich praw?
@maximilianan praw nie, ale sama kultura w którą takie rzeczy są wpisane jest dla mnie obrzydliwa - stąd moja fobia. Dla nich są to rzeczy niedopuszczalne i walczą o to nawet nie mając mocy prawnej. Chodzi nawet o małe gesty, jak odmowa podania dłoni kobiecie.
Zaloguj się aby komentować
Sprawa utknęła w martwym punkcie, teraz będą się dupić z dostępem do odsłuchu i cyk za 10 lat może poznamy wyrok.
@maximilianan aż bym złośliwie zapytał któż to nałożył takie klauzule tajności i co tam w tych nagraniach takiego jest, że ktoś postanowił takie klauzule nałożyć
Zaloguj się aby komentować
Nowy Audyt Obywatelski pokazuje bardzo wysoki poziom patologii w policji. Jeszcze nie najwyższy, bo zatrzymany przeżył, ale bardzo, bardzo wysoki.
Edit: jeden policjant sam sobie wycelował pistolet w głowę w pewnym momencie :v
https://www.youtube.com/watch?v=mpGtDHl6r44&ab_channel=audytobywatelski
#audytobywatelski #policja
@maximilianan W czasach covidu przysrali się do mojego tatusia, gdzie przepisy jasno mówiły, że nie trzeba było mieć wtedy maseczki w parku. I do Pimpka się jeszcze przysrali, do 10 kg kundelka na smyczy. Jebańcy nawet nakłamali w notatce służbowej - bo tatulka zaczepiło czterech gestapowców a w notatce było wymienionych tylko dwóch. Co lepsze tego samego dnia były protesty antymaseczkowe dosłownie kawałek dalej. Nawet żulom chlejącym ławkę dalej wtedy upomnienia nie dali.
Wygrałem mu to w sądzie, on czasem uparty (stary kierowca) i wtedy nie przyjął mandatu. I miał rację.
@vredo a co było ze słynnym sierżantem rybom? To samo. Przylazł melepeta jeden z drugim, napuszony że tylko piórek pawich mu wsadzonych w dupę brakowało i jak jakiś wielki pan życia i śmierci zaczął ludzi straszyć, że mają mu kurwa pokazać paragon z budy z rybami bo inaczej ich aresztuje za jakieś kurwa zgromadzenie xD A jak chuj usłyszał, żeby wypierdalał zrobić raz coś pożytecznego w życiu to się do nagrywającego zesrał i go zaczął straszyć, że "zgaś to bo się zobaczymy w sądzie hur zobaczysz dur". I takie totalnie bezwartościowe miernoty potem płaczą, że oni się szacunku domagają, że upadek społeczeństwa, bo nikt ich już nie szanuje i w ogóle pRoTeCt AnD sErVe. I pomyśleć, że sami sobie przez ostatnie +10 lat ciężko zapracowali, żeby wrócić do punktu wyjścia, z którego mozolnie od upadku komuny starali się odejść żeby pokazać, że się zmienili i wypracowali współczesne standardy.
@maximilianan oj tam pierdolenie. Dobrze go wzięli, szukał sensacji i się doszukal. To jest jak dyskusja w/na ukrainie
@maximilianan murem za polskim mundurem
@radziol niestety niektórzy powinni mundur oddać i przeprosić.
Zaloguj się aby komentować
@maximilianan ziom co sobie foke kupil
Zaloguj się aby komentować